自动机
OI 中所说的「自动机」一般都指「确定有限状态自动机」。
自动机是 OI、计算机科学中被广泛使用的一个数学模型,其思想在许多字符串算法中都有涉及,因此推荐在学习一些字符串算法(KMP、AC 自动机、SAM)前先完成自动机的学习。学习自动机有助于理解上述算法。
前置知识
- 基础图论。
自动机入门
首先理解一下自动机是用来干什么的:自动机是一个对信号序列进行判定的数学模型。
这句话涉及到的名词比较多,逐一解释一下。「信号序列」是指一连串有顺序的信号,例如字符串从前到后的每一个字符、数组从 1 到 n 的每一个数、数从高到低的每一位等。「判定」是指针对某一个命题给出或真或假的回答。有时我们需要对一个信号序列进行判定。一个简单的例子就是判定一个二进制数是奇数还是偶数,较复杂的例子例如判定一个字符串是否回文,判定一个字符串是不是某个特定字符串的子序列等等。
自动机的工作原理和地图很类似。假设你在你家,然后你从你家到学校,按顺序经过了很多路口。每个路口都有岔路,而你在所有这些路口的选择就构成了一个序列。
例如,你的选择序列是「家门 -> 右拐 -> 萍水西街 -> 尚园街 -> 古墩路 -> 地铁站 -> 下宁桥」,那你按顺序经过的路口可能是「家 -> 家门口 -> 萍水西街竞舟北路口 -> 萍水西街尚圆街路口 -> 尚园街古墩路口 -> 古墩路中 -> 三坝地铁站 -> 下宁桥地铁站」。可以发现,上学的选择序列不止这一个。同样要去地铁站,你还可以从竞舟北路绕道,或者横穿文鼎苑抄近路。
而我们如果找到一个选择序列,就可以在地图上比划出这个选择序列能不能去学校。比如,如果一个选择序列是「家门 -> 右拐 -> 萍水西街 -> 尚园街 -> 古墩路 -> 地铁站 -> 钱江路 -> 四号线站台 -> 联庄」,那么它就不会带你去同一个学校,但是仍旧可能是一个可被接受的序列,因为目标地点可能不止一个。
也就是说,我们通过这个地图和一组目的地,将信号序列分成了三类,一类是无法识别的信号序列(例如「家门 -> ???」),一类是能去学校的信号序列,另一类是不能的信号序列。我们将所有合法的信号序列分成了两类,完成了一个判定问题。
既然自动机是一个数学模型,那么显然不可能是一张地图。对地图进行抽象之后,可以简化为一个有向图。因此,自动机的结构就是一张有向图。
而自动机的工作方式和流程图类似,不同的是:自动机的每一个结点都是一个判定结点;自动机的结点只是一个单纯的状态而非任务;自动机的边可以接受多种字符(不局限于 T 或 F)。
例如,完成「判断一个二进制数是不是偶数」的自动机如下:
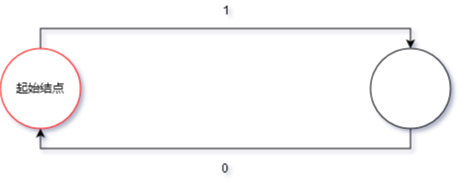
从起始结点开始,从高到低接受这个数的二进制序列,然后看最终停在哪里。如果最终停在红圈结点,则是偶数,否则不是。
如果需要判定一个有限的信号序列和另外一个信号序列的关系(例如另一个信号序列是不是某个信号序列的子序列),那么常用的方法是针对那个有限的信号序列构建一个自动机。这个在学习 KMP 的时候会讲到。
需要注意的是,自动机只是一个 数学模型,而 不是算法,也 不是数据结构。实现同一个自动机的方法有很多种,可能会有不一样的时空复杂度。
接下来你可以选择继续看自动机的形式化定义,也可以去学习 KMP、AC 自动机 或 SAM。
形式化定义
一个 确定有限状态自动机(DFA) 由以下五部分构成:
- 字符集(
- 状态集合(
- 起始状态(
- 接受状态集合(
- 转移函数(
DFA 的作用就是识别字符串,一个自动机
当一个 DFA 读入一个字符串时,从初始状态起按照转移函数一个一个字符地转移。如果读入完一个字符串的所有字符后位于一个接受状态,那么我们称这个 DFA 接受 这个字符串,反之我们称这个 DFA 不接受 这个字符串。
如果一个状态
我们扩展定义转移函数
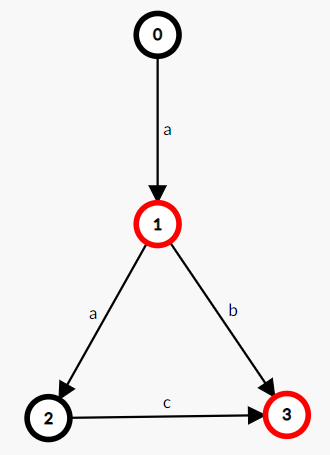
如,一个接受且仅接受字符串 "a", "ab", "aac" 的 DFA:
OI 中常用的自动机
字典树
字典树 是大部分 OIer 接触到的第一个自动机,接受且仅接受指定的字符串集合中的元素。
转移函数就是 Trie 上的边,接受状态是将每个字符串插入到 Trie 时到达的那个状态。
KMP 自动机
KMP 算法 可以视作自动机,基于字符串
转移函数:
AC 自动机
AC 自动机 接受且仅接受以指定的字符串集合中的某个元素为后缀的字符串。也就是 Trie + KMP。
后缀自动机
后缀自动机 接受且仅接受指定字符串的后缀。
广义后缀自动机
广义后缀自动机 接受且仅接受指定的字符串集合中的某个元素的后缀。也就是 Trie + SAM。
广义 SAM 与 SAM 的关系就是 AC 自动机与 KMP 自动机的关系。
回文自动机
回文自动机 比较特殊,它不能非常方便地定义为自动机。
如果需要定义的话,它接受且仅接受某个字符串的所有回文子串的 中心及右半部分。
「中心及右边部分」在奇回文串中就是字面意思,在偶回文串中定义为一个特殊字符加上右边部分。这个定义看起来很奇怪,但它能让 PAM 真正成为一个自动机,而不仅是两棵树。
序列自动机
序列自动机 接受且仅接受指定字符串的子序列。
后缀链接
由于自动机和匹配有着密不可分的关系,而匹配的一个基本思想是「这个串不行,就试试它的后缀可不可以」,所以在很多自动机(KMP、AC 自动机、SAM、PAM)中,都有后缀链接的概念。
一个状态会对应若干字符串,而这个状态的后缀链接,是在自动机上的、是这些字符串的公共真后缀的字符串中,最长的那一个。
一般来讲,后缀链接会形成一棵树,并且不同自动机的后缀链接树有着一些相同的性质,学习时可以加以注意。
扩展阅读
在计算复杂性领域中,自动机是一个经典的模型。并且,自动机与正则语言有着密不可分的关系。
如果对相关内容感兴趣的话,推荐阅读博客 计算复杂性(1)Warming Up: 自动机模型。
本页面最近更新:2023/3/22 15:46:23,更新历史
发现错误?想一起完善? 在 GitHub 上编辑此页!
本页面贡献者:CCXXXI, countercurrent-time, Enter-tainer, FFjet, H-J-Granger, Ir1d, mgt, NachtgeistW, orzAtalod, ouuan, ouuan, SukkaW
本页面的全部内容在 CC BY-SA 4.0 和 SATA 协议之条款下提供,附加条款亦可能应用