爬山算法
简介
爬山算法是一种局部择优的方法,采用启发式方法,是对深度优先搜索的一种改进,它利用反馈信息帮助生成解的决策。
直白地讲,就是当目前无法直接到达最优解,但是可以判断两个解哪个更优的时候,根据一些反馈信息生成一个新的可能解。
因此,爬山算法每次在当前找到的最优方案
这种算法对于单峰函数显然可行。
Q:都知道是单峰函数了为什么不三分呢?
A:爬山算法的优势在于当正解的写法你并不了解(常见于毒瘤计算几何和毒瘤数学题),或者本身状态维度很多,无法容易地写分治(例 2 就可以用二分完成合法正解)时,可以通过非常暴力的计算得到最优解。
但是对于多数需要求解的函数,爬山算法很容易进入一个局部最优解,如下图(最优解为
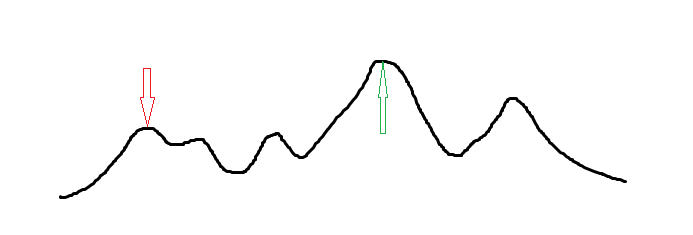
具体实现
爬山算法一般会引入温度参数(类似模拟退火)。类比地说,爬山算法就像是一只兔子喝醉了在山上跳,它每次都会朝着它所认为的更高的地方(这往往只是个不准确的趋势)跳,显然它有可能一次跳到山顶,也可能跳过头翻到对面去。不过没关系,兔子翻过去之后还会跳回来。显然这个过程很没有用,兔子永远都找不到出路,所以在这个过程中兔子冷静下来并在每次跳的时候更加谨慎,少跳一点,以到达合适的最优点。
兔子逐渐变得清醒的过程就是降温过程,即温度参数在爬山的时候会不断减小。
关于降温:降温参数是略小于
例 1 「JSOI2008」球形空间产生器
题意:给出
很明显的单峰函数,可以使用爬山解决。本题算法流程:
- 初始化球心为各个给定点的重心(即其各维坐标均为所有给定点对应维度坐标的平均值),以减少枚举量。
- 对于当前的球心,求出每个已知点到这个球心欧氏距离的平均值。
- 遍历所有已知点。记录一个改变值
- 将我们记录的
- 在温度小于某个给定阈值的时候结束。
因此,我们在更新球心的时候,不能直接加上改变值,而是要加上改变值与温度的乘积。
并不是每一道爬山题都可以具体地用温度解决,这只是一个例子。
例题参考代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 | |
例 2 「BZOJ 3680」吊打 XXX
题意:求
框架类似,用了点物理知识。
参考代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 | |
优化
很容易想到的是,为了尽可能获取优秀的答案,我们可以多次爬山。方法有修改初始状态/修改降温参数/修改初始温度等,然后开一个全局最优解记录答案。每次爬山结束之后,更新全局最优解。
这样处理可能会存在的问题是超时,在正式考试时请手造大数据测试调参。
劣势
其实爬山算法的劣势上文已经提及:它容易陷入一个局部最优解。当目标函数不是单峰函数时,这个劣势是致命的。因此我们要引进 模拟退火。
本页面最近更新:2023/9/1 16:49:46,更新历史
发现错误?想一起完善? 在 GitHub 上编辑此页!
本页面贡献者:abc1763613206, countercurrent-time, Early0v0, EarthMessenger, Enter-tainer, H-J-Granger, Henry-ZHR, Ir1d, kenlig, ksyx, Marcythm, NachtgeistW, ouuan, REM_001, Siyuan, sshwy, SukkaW, Tiphereth-A, zyouxam
本页面的全部内容在 CC BY-SA 4.0 和 SATA 协议之条款下提供,附加条款亦可能应用