二次剩余
引入
二次剩余可以认为是在讨论求模意义下 开平方 运算的可行性。对于更高次方的开方可参见 k 次剩余。
定义
二次剩余
令整数
则称
Euler 判别法
当模数为奇素数时,我们有如下定理:
Euler 判别法
对奇素数
即对上述的
证明
首先由 Fermat 小定理 有
从而对任意满足
另外由
其中
由 同余方程的定理 5 可知,
基于 Euler 判别法,我们可以得到如下推论:
二次剩余的数量
对于奇素数
Legendre 符号
为了方便接下来的讨论,我们引入如下记号:
Legendre 符号
对 奇素数
即对于
下表为部分 Legendre 符号的值(From Wikipedia)
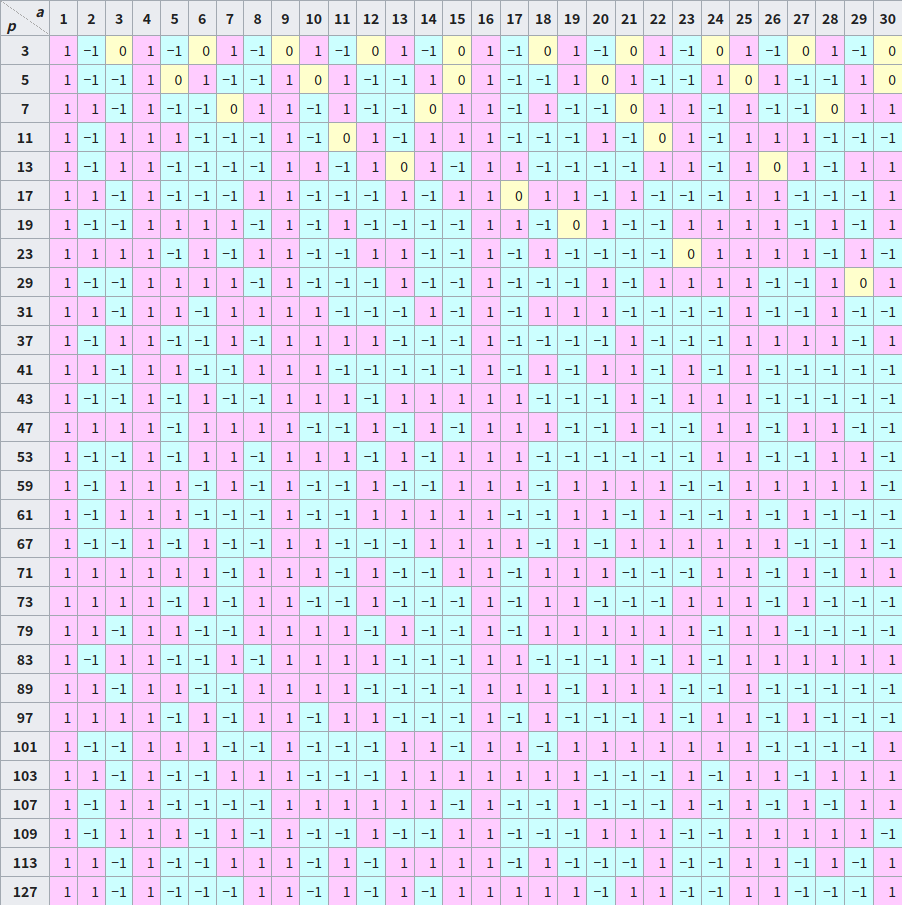
性质
对任意整数
进一步,我们有推论:
(完全积性)对任意整数
我们有推论:对整数
证明
- 由 Legendre 符号的定义 和 Euler 判别法 易得。
注意到
而
由 1 得
而
参见 二次互反律
基于如上性质,若对任意奇素数
二次互反律
二次互反律
设
证明方式很多5。一种证明方式是基于如下引理:
Gauss 引理
设
证明
设
我们知道对
即
从而由 Legendre 符号的 性质 1 即得证。
容易得到如下推论:
推论
对奇素数
对奇素数
证明
对 Gauss 引理中的
因此
若
若
根据如上推论,证明二次互反律只需验证
考虑由点
二次互反律不仅能用于判断数
Example
- 使得
- 使得
- 使得
另外,我们还可以证明诸如「形如
Jacobi 符号
根据二次互反律,我们可以很自然地想到一种推广 Legendre 符号的方法:
Warning
我们一般不区分 Legendre 符号和 Jacobi 符号,因为由完全积性可知 Jacobi 符号具有和 Legendre 符号一样的性质,所以这两种符号的计算方法是一致的。但是有一点需要注意:当
我们还可以把模数进一步推广为 整数(只需补充
相关算法
特殊情况时的算法
对于同余方程
那么
Atkin 算法
仍然考虑上述同余方程,此时
证明
那么
Cipolla 算法
Cipolla 算法用于求解同余方程
算法可描述为找到
在复数域
后文考虑对于系数属于有限域
选择
若
证明
令
又因为二项式定理
可以发现只有当
所以
若
所以
Bostan–Mori 算法
该算法基于 Cipolla 算法,我们将问题转换为 常系数齐次线性递推 再应用 Bostan–Mori 算法。考虑另一种常见的 Cipolla 算法的描述为
且
而
Legendre 算法
对于同余方程
证明
考虑选择一个
存在环态射
那么
所以
Tonelli–Shanks 算法
Tonelli–Shanks 算法是基于离散对数求解同余方程
令
证明
而
所以
若
所以
剩下的问题是如何计算
因为
正确性显然。
习题
参考资料与注释
Daniel. J. Bernstein. Faster Square Roots in Annoying Finite Fields. ↩
S. Müller, On the computation of square roots in finite fields, Design, Codes and Cryptography, Vol.31, pp. 301-312, 2004 ↩
A. Menezes, P. van Oorschot and S. Vanstone. Handbook of Applied Cryptography, 1996. ↩
Alin Bostan, Ryuhei Mori.A Simple and Fast Algorithm for Computing the N-th Term of a Linearly Recurrent Sequence. ↩
本页面最近更新:2025/6/29 23:20:23,更新历史
发现错误?想一起完善? 在 GitHub 上编辑此页!
本页面贡献者:hly1204, ShaoChenHeng, Chrogeek, Enter-tainer, Great-designer, iamtwz, monkeysui, nanmenyangde, sshwy, StudyingFather, TachikakaMin, Tiphereth-A, Xeonacid, xyf007, c-forrest, rgw2010
本页面的全部内容在 CC BY-SA 4.0 和 SATA 协议之条款下提供,附加条款亦可能应用