跳转至

分拆数

分拆：将自然数 写成递降正整数和的表示。

和式中每个正整数称为一个部分。

分拆数：。自然数 的分拆方法数。

自 开始的分拆数：

n012345678
112357111522

k 部分拆数

将 分成恰有 个部分的分拆，称为 部分拆数，记作 。

显然， 部分拆数 同时也是下面方程的解数：

如果这个方程里面恰有 个部分非 0，则恰有 个解。因此有和式：

相邻两个和式作差，得：

如果列出表格，每个格里的数，等于左上方的数，加上该格向上方数，所在列数个格子中的数。

k012345678
100000000
010000000
011000000
011100000
012110000
012211000
013321100
013432110
014553211

例题

计算 k 部分拆数

计算 部分拆数 。多组输入，其中 上界为 ， 上界为 ，对 取模。

观察表格与递推式，按列更新对于存储更有利。不难写出程序：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <cstdio>
#include <cstring>

int p[10005][1005]; /*将自然数n分拆为k个部分的方法数*/

int main() {
  int n, k;
  while (~scanf("%d%d", &n, &k)) {
    memset(p, 0, sizeof(p));
    p[0][0] = 1;
    int i;
    for (i = 1; i <= n; ++i) {
      int j;
      for (j = 1; j <= k; ++j) {
        if (i - j >= 0) /*p[i-j][j]所有部分大于1*/
        {
          p[i][j] = (p[i - j][j] + p[i - 1][j - 1]) %
                    1000007; /*p[i-1][j-1]至少有一个部分为1。*/
        }
      }
    }
    printf("%d\n", p[n][k]);
  }
}

生成函数

由等比数列求和公式，有：

对于 部分拆数，生成函数稍微复杂。具体写出如下：

Ferrers 图

Ferrers 图：将分拆的每个部分用点组成的行表示。每行点的个数为这个部分的大小。

根据分拆的定义，Ferrers 图中不同的行按照递减的次序排放。最长行在最上面。

例如：分拆 的 Ferrers 图。

将一个 Ferrers 图沿着对角线翻转，得到的新 Ferrers 图称为原图的共轭，新分拆称为原分拆的共轭。显然，共轭是对称的关系。

例如上述分拆 的共轭是分拆 。

最大 分拆数：自然数 的最大部分为 的分拆个数。

根据共轭的定义，有显然结论：

最大 分拆数与 部分拆数相同，均为 。

互异分拆数

互异分拆数：。自然数 的各部分互不相同的分拆方法数。（Different）

n012345678
111223456

同样地，定义互异 部分拆数 ，表示最大拆出 个部分的互异分拆，是这个方程的解数：

完全同上，也是这个方程的解数：

这里与上面不同的是，由于互异，新方程中至多只有一个部分为零。有不变的结论：恰有 个部分非 ，则恰有 个解，这里 只取 或 。因此直接得到递推：

同样像组合数一样列出表格，每个格里的数，等于该格前一列上数，所在列数个格子中的数，加上该格向上方数，所在列数个格子中的数。

k012345678
100000000
010000000
010000000
011000000
011000000
012000000
012100000
013100000
013200000

例题

计算互异分拆数

计算互异分拆数 。多组输入，其中 上界为 ，对 取模。

观察表格与递推式，按列更新对于存储更有利。代码中将后一位缩减了空间，仅保留相邻两项。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <cstdio>
#include <cstring>

int pd[50005][2]; /*将自然数n分拆为k个部分的互异方法数*/

int main() {
  int n;
  while (~scanf("%d", &n)) {
    memset(pd, 0, sizeof(pd));
    pd[0][0] = 1;
    int ans = 0;
    int j;
    for (j = 1; j < 350; ++j) {
      int i;
      for (i = 0; i < 350; ++i) {
        pd[i][j & 1] = 0; /*pd[i][j]只与pd[][j]和pd[][j-1]有关*/
      }
      for (i = 0; i <= n; ++i) {
        if (i - j >= 0) /*pd[i-j][j]所有部分大于1*/
        {
          pd[i][j & 1] = (pd[i - j][j & 1] + pd[i - j][(j - 1) & 1]) %
                         1000007; /*pd[i-j][j-1]至少有一个部分为1。*/
        }
      }
      ans = (ans + pd[n][j & 1]) % 1000007;
    }
    printf("%d\n", ans);
  }
}

奇分拆数

奇分拆数：。自然数 的各部分都是奇数的分拆方法数。（Odd）

有一个显然的等式：

最左边是互异分拆数的生成函数，最右边是奇分拆数的生成函数。两者对应系数相同，因此，奇分拆数和互异分拆数相同：

但显然 部奇分拆数和互异 部分拆数不是一个概念，这里就不列出了。

再引入两个概念：

互异偶分拆数：。自然数 的部分数为偶数的互异分拆方法数。（Even）

互异奇分拆数：。自然数 的部分数为奇数的互异分拆方法数。（Odd）

因此有：

同样也有相应的 部概念。由于过于复杂，不再列出。

五边形数定理

单独观察分拆数的生成函数的分母部分：

将这部分展开，可以想到互异分拆，与互异分拆拆出的部分数奇偶性有关。

具体地，互异偶部分拆在展开式中被正向计数，互异奇部分拆在展开式中被负向计数。因此展开式中各项系数为两方法数之差。即：

接下来说明，多数情况下，上述两方法数相等，在展开式中系数为 ；仅在少数位置，两方法数相差 或 。

这里可以借助构造对应的办法。

画出每个互异分拆的 Ferrers 图。最后一行称为这个图的底，底上点的个数记为 （Bottom）；连接最上面一行的最后一个点与图中某点的最长 度角线段，称为这个图的坡，坡上点的个数记为 （Slide）。

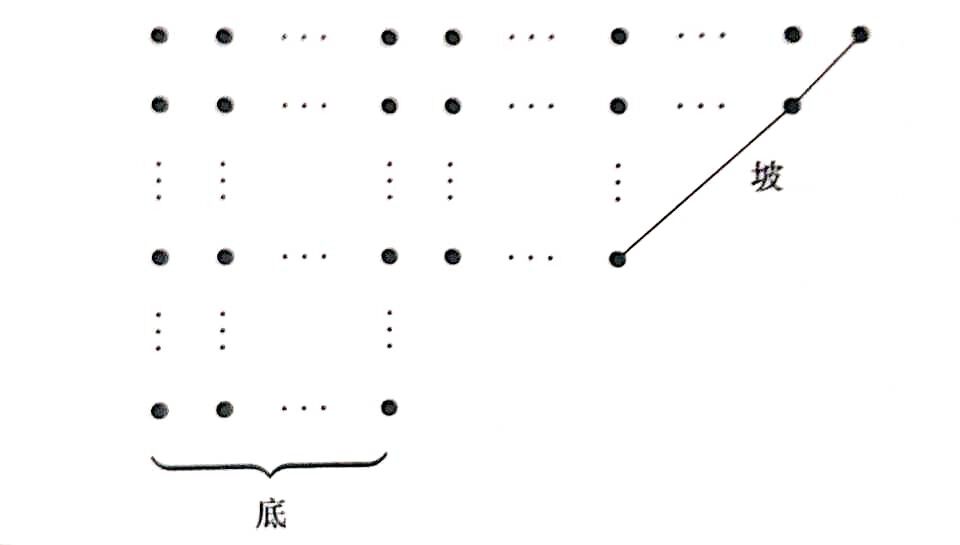
要想在互异偶部分拆与互异奇部分拆之间构造对应，就要定义变换，在保证互异条件不变的前提下，使得行数改变 ：

变换 A：当 小于等于 的时候，就将底移到右边，成为一个新坡。

变换 B：当 大于 的时候，就将坡移到下边，成为一个新底。

这两个变换对于大多数 的任意互异分拆，恰有一个变换可以进行，就在互异偶部分拆与互异奇部分拆之间构造了一个一一对应。已经构造了一一对应的两部分分拆个数相等，因此这时展开式中第 项系数为 。

但是对于某些 ，其存在恰一个互异分拆无法进行上述变换。

  • 情况一： 且底与坡有一个公共点时，变换 A 不能进行。此时

展开式的第 项与分拆部分数的奇偶性有关，为 。

  • 情况二： 且底与坡有一个公共点时，变换 B 不能进行。此时

展开式的第 项为 。

用 替换上式的 ，得到 ，其中 为负整数，展开式的第 项仍为 。。

由于两种情况不会在同一个 同时出现，我们可以把两个条件合起来，得到 需要满足的条件是

至此，我们就证明了：

回忆一下：这个式子是分拆数的生成函数的倒数，因此其与分拆数的生成函数相乘的结果是 。整理并对比两边各项系数，就得到分拆数数列的递推式。

这个递推式有无限项，但是如果规定负数的分拆数是 （ 的分拆数已经定义为 ），那么就简化为了有限项。

例题

计算分拆数

计算分拆数 。多组输入，其中 上界为 ，对 取模。

采用五边形数定理的方法。有代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <cstdio>

long long a[100010];
long long p[50005];

int main() {
  p[0] = 1;
  p[1] = 1;
  p[2] = 2;
  int i;
  for (i = 1; i < 50005;
       i++) /*递推式系数1,2,5,7,12,15,22,26...i*(3*i-1)/2,i*(3*i+1)/2*/
  {
    a[2 * i] = i * (i * 3 - 1) / 2; /*五边形数为1,5,12,22...i*(3*i-1)/2*/
    a[2 * i + 1] = i * (i * 3 + 1) / 2;
  }
  for (
      i = 3; i < 50005;
      i++) /*p[n]=p[n-1]+p[n-2]-p[n-5]-p[n-7]+p[12]+p[15]-...+p[n-i*[3i-1]/2]+p[n-i*[3i+1]/2]*/
  {
    p[i] = 0;
    int j;
    for (j = 2; a[j] <= i; j++) /*有可能为负数,式中加1000007*/
    {
      if (j & 2) {
        p[i] = (p[i] + p[i - a[j]] + 1000007) % 1000007;
      } else {
        p[i] = (p[i] - p[i - a[j]] + 1000007) % 1000007;
      }
    }
  }
  int n;
  while (~scanf("%d", &n)) {
    printf("%lld\n", p[n]);
  }
}
本页面最近更新：2024/11/23 15:23:11，更新历史
发现错误？想一起完善？ 在 GitHub 上编辑此页！
本页面贡献者：2008verser, Early0v0, Great-designer, Ir1d, ksyx, myeeye, Tiphereth-A, YOYO-UIAT
本页面的全部内容在 CC BY-SA 4.0 和 SATA 协议之条款下提供，附加条款亦可能应用