容斥原理

引入

是 $10+15+21=46$ 个吗？不是的，因为有些学生可能同时喜欢数学和语文，或者语文和编程，甚至还有可能三者都喜欢。

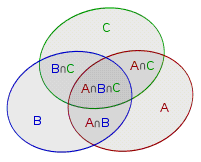
为了叙述方便，我们把喜欢语文、数学、编程的学生集合分别用 $A,B,C$ 表示，则学生总数等于 $|A\cup B\cup C|$。刚才已经讲过，如果把这三个集合的元素个数 $|A|,|B|,|C|$ 直接加起来，会有一些元素重复统计了，因此需要扣掉 $|A\cap B|,|B\cap C|,|C\cap A|$，但这样一来，又有一小部分多扣了，需要加回来，即 $|A\cap B\cap C|$。即

$$|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|B\cap C|-|C\cap A|+|A\cap B\cap C|$$

把上述问题推广到一般情况，就是我们熟知的容斥原理。

定义

设 U 中元素有 n 种不同的属性，而第 i 种属性称为 $P_i$，拥有属性 $P_i$ 的元素构成集合 $S_i$，那么

即

证明

对于每个元素使用二项式定理计算其出现的次数。对于元素 x，假设它出现在 $T_1,T_2,\cdots ,T_m$ 的集合中，那么它的出现次数为

于是每个元素出现的次数为 1，那么合并起来就是并集。证毕。

补集

对于全集 U 下的 集合的并 可以使用容斥原理计算，而集合的交则用全集减去 补集的并集 求得：

$$\left|\bigcap _{i=1}^n{S}_i\right|=|U|-\left|\bigcup _{i=1}^n\overline{S_i}\right|$$

右边使用容斥即可。

可能接触过容斥的读者都清楚上述内容，而更关心的是容斥的应用。

那么接下来我们给出 3 个层次不同的例题来为大家展示容斥原理的应用。

不定方程非负整数解计数

没有限制时

如果没有 $x_i\le b_i$ 的限制，那么不定方程 $\sum _{i=1}^n{x}_i=m$ 的非负整数解的数目为 ${\displaystyle (\genfrac{}{}{0ex}{}{m+n-1}{n-1})}$.

略证：插板法。

相当于你有 $m$ 个球要分给 $n$ 个盒子，允许某个盒子是空的。这个问题不能直接用组合数解决。

于是我们再加入 $n-1$ 个球，于是问题就变成了在一个长度为 $m+n-1$ 的球序列中选择 $n-1$ 个球，然后这个 $n-1$ 个球把这个序列隔成了 $n$ 份，恰好可以一一对应放到 $n$ 个盒子中。那么在 $m+n-1$ 个球中选择 $n-1$ 个球的方案数就是 ${\displaystyle (\genfrac{}{}{0ex}{}{m+n-1}{n-1})}$。

容斥模型

接着我们尝试抽象出容斥原理的模型：

1. 全集 U：不定方程 $\sum _{i=1}^n{x}_i=m$ 的非负整数解
2. 元素：变量 $x_i$.
3. 属性：$x_i$ 的属性即 $x_i$ 满足的条件，即 $x_i\le b_i$ 的条件

目标：所有变量满足对应属性时集合的大小，即 $|\bigcap _{i=1}^n{S}_i|$.

这个东西可以用 $\left|\bigcap _{i=1}^n{S}_i\right|=|U|-\left|\bigcup _{i=1}^n\overline{S_i}\right|$ 求解。$|U|$ 可以用组合数计算，后半部分自然使用容斥原理展开。

那么问题变成，对于一些 $\overline{S_{a_i}}$ 的交集求大小。考虑 $\overline{S_{a_i}}$ 的含义，表示 $x_{a_i}\ge b_{a_i}+1$ 的解的数目。而交集表示同时满足这些条件。因此这个交集对应的不定方程中，有些变量有 下界限制，而有些则没有限制。

能否消除这些下界限制呢？既然要求的是非负整数解，而有些变量的下界又大于 $0$，那么我们直接 把这个下界减掉，就可以使得这些变量的下界变成 $0$，即没有下界啦。因此对于

的不定方程形式为

$$\sum _{i=1}^n{x}_i=m-\sum _{i=1}^k(b_{a_i}+1)$$

于是这个也可以组合数计算啦。这个长度为 $k$ 的 $a$ 数组相当于在枚举子集。

HAOI2008 硬币购物

如果用背包做的话复杂度是 $O(4nS)$，无法承受。这道题最明显的特点就是硬币一共只有四种。抽象模型，其实就是让我们求方程 $\sum _{i=1}^4{C}_i{x}_i=S,x_i\le D_i$ 的非负整数解的个数。

采用同样的容斥方式，$x_i$ 的属性为 $x_i\le D_i$. 套用容斥原理的公式，最后我们要求解

$$\sum _{i=1}^4{C}_i{x}_i=S-\sum _{i=1}^k{C}_{a_i}(D_{a_i}+1)$$

也就是无限背包问题。这个问题可以预处理，算上询问，总复杂度 $O(4S+2^{4}n)$。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

#include <iostream>
using namespace std;
constexpr long long S = 1e5 + 5;
long long c[5], d[5], n, s;
long long f[S];

int main() {
  cin.tie(nullptr)->sync_with_stdio(false);
  cin >> c[1] >> c[2] >> c[3] >> c[4] >> n;
  f[0] = 1;
  for (long long j = 1; j <= 4; j++)
    for (long long i = 1; i < S; i++)
      if (i >= c[j]) f[i] += f[i - c[j]];  // f[i]：价格为i时的硬币组成方法数
  for (long long k = 1; k <= n; k++) {
    cin >> d[1] >> d[2] >> d[3] >> d[4] >> s;
    long long ans = 0;
    for (long long i = 1; i < 16;
         i++) {  // 容斥，因为物品一共有4种，所以从1到2^4-1=15循环
      long long m = s, bit = 0;
      for (long long j = 1; j <= 4; j++) {
        if ((i >> (j - 1)) % 2 == 1) {
          m -= (d[j] + 1) * c[j];
          bit++;
        }
      }
      if (m >= 0) ans += (bit % 2 * 2 - 1) * f[m];
    }
    cout << f[s] - ans << '\n';
  }
  return 0;
}

完全图子图染色问题

前面的三道题都是容斥原理的正向运用，这道题则需要用到容斥原理逆向分析。

数学形式

一看这道题的算法趋向并不明显，因此对于棘手的题目首先抽象出数学形式。得分差即为奇偶对称差，可以用 -1 的幂次来作为系数。我们求的是

$$Ans=\sum _{S\subseteq E}(-1{)}^{|S|-1}F(S)$$

容斥模型

相邻结点染同一种颜色，我们把它当作属性。在这里我们先不遵守染色的规则，假定我们用 m 种颜色直接对图染色。对于图 $G^{\prime }=(V,S)$，我们把它当作 元素。属性 $x_i=x_j$ 的含义是结点 i,j 染同色（注意，并未要求 i,j 之间有连边）。

而属性 $x_i=x_j$ 对应的 集合 定义为 $Q_{i,j}$，其含义是所有满足该属性的图 $G^{\prime }$ 的染色方案，集合的大小就是满足该属性的染色方案数，集合内的元素相当于所有满足该属性的图 $G^{\prime }$ 的染色图。

回到题目，「相邻的结点必须染同一种颜色」，可以理解为若干个 $Q$ 集合的交集。因此可以写出

$$F(S)=\left|\bigcap _{(i,j)\in S}{Q}_{i,j}\right|$$

上述式子右边的含义就是说对于 S 内的每一条边 $(i,j)$ 都满足 $x_i=x_j$ 的染色方案数，也就是 $F(S)$.

是不是很有容斥的味道了？由于容斥原理本身没有二元组的形式，因此我们把 所有 的边 $(i,j)$ 映射到 $T=\frac{n(n+1)}{2}$ 个整数上，假设将 $(i,j)$ 映射为 $k,1\le k\le T$，同时 $Q_{i,j}$ 映射为 $Q_k$. 那么属性 $x_i=x_j$ 则定义为 $P_k$.

同时 S 可以表示为若干个 k 组成的集合，即 $S⟺K=\{k_1,k_2,\cdots ,k_m\}$.（也就是说我们在边集与数集间建立了等价关系）。

而 E 对应集合 $M=\{1,2,\cdots ,\frac{n(n+1)}{2}\}$. 于是乎

$$F(S)⟺F(\{k_i\})=\left|\bigcap _{k_i}{Q}_{k_i}\right|$$

逆向分析

那么要求的式子展开

于是就出现了容斥原理的展开形式，因此对这个式子逆向推导

$$Ans=\left|\bigcup _{i=1}^T{Q}_i\right|$$

再考虑等式右边的含义，只要满足 $1\sim T$ 任一条件即可，也就是存在两个点同色（不一定相邻）的染色方案数！而我们知道染色方案的全集是 $U$，显然 $|U|=m^n$. 而转化为补集，就是求两两异色的染色方案数，即 $A_m^n=\frac{m!}{(m-n)!}$. 因此

$$Ans=m^n-A_m^n$$

解决这道题，我们首先抽象出题目数学形式，然后从题目中信息量最大的条件，$F(S)$ 函数的定义入手，将其转化为集合的交并补。然后将式子转化为容斥原理的形式，并 逆向推导 出最终的结果。这道题体现的正是容斥原理的逆用。

数论中的容斥

使用容斥原理能够巧妙地求解一些数论问题。

容斥原理求最大公约数为 k 的数对个数

考虑下面的问题：

求最大公约数为 $k$ 的数对个数

设 $1\le x,y\le N$，$f(k)$ 表示最大公约数为 $k$ 的有序数对 $(x,y)$ 的个数，求 $f(1)$ 到 $f(N)$ 的值。

这道题固然可以用欧拉函数或莫比乌斯反演的方法来做，但是都不如用容斥原理来的简单。

由容斥原理可以得知，先找到所有以 $k$ 为 公约数 的数对，再从中剔除所有以 $k$ 的倍数为 公约数 的数对，余下的数对就是以 $k$ 为 最大公约数 的数对。即 $f(k)=$ 以 $k$ 为 公约数 的数对个数 $-$ 以 $k$ 的倍数为 公约数 的数对个数。

进一步可发现，以 $k$ 的倍数为 公约数 的数对个数等于所有以 $k$ 的倍数为 最大公约数 的数对个数之和。于是，可以写出如下表达式：

$$f(k)=\lfloor (N/k){\rfloor }^2-\sum _{i=2}^{i\ast k\le N}f(i\ast k)$$

由于当 时，我们可以直接算出 $f(k)=\lfloor (N/k){\rfloor }^2$，因此我们可以倒过来，从 $f(N)$ 算到 $f(1)$ 就可以了。于是，我们使用容斥原理完成了本题。

1
2
3
4

for (long long k = N; k >= 1; k--) {
  f[k] = (N / k) * (N / k);
  for (long long i = k + k; i <= N; i += k) f[k] -= f[i];
}

上述方法的时间复杂度为 $O(\sum _{i=1}^{N}N/i)=O(N\sum _{i=1}^{N}1/i)=O(N\log N)$。

附赠三倍经验供大家练手。

• Luogu P2398 GCD SUM
• Luogu P2158[SDOI2008] 仪仗队
• Luogu P1447[NOI2010] 能量采集

容斥原理推导欧拉函数

考虑下面的问题：

直接计算是 $O(n\log n)$ 的，用线性筛是 $O(n)$ 的，杜教筛是 $O(n^{\frac{2}{3}})$ 的（话说一道数论入门题用容斥做为什么还要扯到杜教筛上），接下来考虑用容斥推出欧拉函数的公式

判断两个数是否互质，首先分解质因数

$$n=\prod _{i=1}^k{p_i}^{c_i}$$

那么就要求对于任意 $p_i$，$x$ 都不是 $p_i$ 的倍数，即 $p_i\nmid x$. 把它当作属性，对应的集合为 $S_i$，因此有

$$\phi (n)=\left|\bigcap _{i=1}^k{S}_i\right|=|U|-\left|\bigcup _{i=1}^k\overline{S_i}\right|$$

全集大小 $|U|=n$，而 $\overline{S_i}$ 表示的是 $p_i\mid x$ 构成的集合，显然 $|\overline{S_i}|=\frac{n}{p_i}$，并由此推出

因此可得

这就是欧拉函数的数学表示啦

容斥原理一般化

容斥原理常用于集合的计数问题，而对于两个集合的函数 $f(S),g(S)$，若

$$f(S)=\sum _{T\subseteq S}g(T)$$

那么就有

$$g(S)=\sum _{T\subseteq S}(-1{)}^{|S|-|T|}f(T)$$

证明

接下来我们简单证明一下。我们从等式的右边开始推：

我们发现后半部分的求和与 $Q$ 无关，因此把后半部分的 $Q$ 剔除：

$$=\sum _{Q}g(Q)\sum _{T\subseteq (S\setminus Q)}(-1{)}^{|S\setminus Q|-|T|}$$

记关于集合 $P$ 的函数 $F(P)=\sum _{T\subseteq P}(-1{)}^{|P|-|T|}$，并化简这个函数：

因此原来的式子的值是

$$\sum _{Q}g(Q)\sum _{T\subseteq (S\setminus Q)}(-1{)}^{|S\setminus Q|-|T|}=\sum _{Q}g(Q)F(S\setminus Q)=\sum _{Q}g(Q)\cdot 0^{|S\setminus Q|}$$

分析发现，仅当 $|S\setminus Q|=0$ 时有 $0^0=1$，这时 $Q=S$，对答案的贡献就是 $g(S)$，其他时侯 $0^{|S\setminus Q|}=0$，则对答案无贡献。于是得到

$$\sum _{Q}g(Q)\cdot 0^{|S\setminus Q|}=g(S)$$

综上所述，得证。

推论

该形式还有这样一个推论。在全集 $U$ 下，对于函数 $f(S),g(S)$，如果

$$f(S)=\sum _{S\subseteq T}g(T)$$

那么

$$g(S)=\sum _{S\subseteq T}(-1{)}^{|T|-|S|}f(T)$$

这个推论其实就是补集形式，证法类似。

DAG 计数

直接 DP

考虑 DP，定义 $f[i,j]$ 表示 $i$ 个点的 DAG，有 $j$ 点个入度为 $0$ 的图的个数。假设去掉这 $j$ 个点后，有 $k$ 个点入度为 $0$，那么在去掉前这 $k$ 个点至少与这 $j$ 个点中的某几个有连边，即 $2^j-1$ 种情况；而这 $j$ 个点除了与 $k$ 个点连边，还可以与剩下的点任意连边，有 $2^{i-j-k}$ 种情况。因此方程如下：

$$f[i,j]=(\genfrac{}{}{0ex}{}{i}{j})\sum _{k=1}^{i-j}(2^j-1{)}^k{2}^{(i-j-k)j}f[i-j,k]$$

计算上式的复杂度是 $O(n^3)$ 的。

放宽限制

上述 DP 的定义是恰好 $j$ 个点入度为 $0$, 太过于严格，可以放宽为至少 $j$ 个点入度为 $0$。直接定义 $f[i]$ 表示 $i$ 个点的 DAG 个数。可以直接容斥。考虑选出的 $j$ 个点，这 $j$ 个点可以和剩下的 $i-j$ 个点有任意的连边，即 ${\left(2^{i-j}\right)}^j=2^{(i-j)j}$ 种情况：

$$f[i]=\sum _{j=1}^i(-1{)}^{j-1}(\genfrac{}{}{0ex}{}{i}{j})2^{(i-j)j}f[i-j]$$

计算上式的复杂度是 $O(n^2)$ 的。

Min-max 容斥

对于满足 全序 关系并且其中元素满足可加减性的序列 $\{x_i\}$，设其长度为 $n$，并设 $S=\{1,2,3,\cdots ,n\}$，则有：

$$\underset{i\in S}{max}{x}_i=\sum _{T\subseteq S}(-1{)}^{|T|-1}\underset{j\in T}{min}{x}_j$$

$$\underset{i\in S}{min}{x}_i=\sum _{T\subseteq S}(-1{)}^{|T|-1}\underset{j\in T}{max}{x}_j$$

证明： 考虑做一个到一般容斥原理的映射。对于 $x\in S$，假设 $x$ 是第 $k$ 小的元素。那么我们定义一个映射 $f:x\mapsto \{1,2,\cdots ,k\}$。显然这是一个双射。

那么容易发现，对于 $x,y\in S$，$f(min(x,y))=f(x)\cap f(y)$，$f(max(x,y))=f(x)\cup f(y)$。因此我们得到：

然后再把 $\left|f\left(\underset{i\in S}{max}{x}_i\right)\right|$ 映射回 $\underset{i\in S}{max}{x}_i$，而 $min$ 是类似的。

证毕。

但是你可能觉得这个式子非常蠢，最大值明明可以直接求。之所以 min-max 容斥这么重要，是因为它在期望上也是成立的，即：

$$E\left(\underset{i\in S}{max}{x}_i\right)=\sum _{T\subseteq S}(-1{)}^{|T|-1}E\left(\underset{j\in T}{min}{x}_j\right)$$

$$E\left(\underset{i\in S}{min}{x}_i\right)=\sum _{T\subseteq S}(-1{)}^{|T|-1}E\left(\underset{j\in T}{max}{x}_j\right)$$

证明： 我们考虑计算期望的一种方法：

$$E\left(\underset{i\in S}{max}{x}_i\right)=\sum _{y}P(y=x)\underset{j\in S}{max}{y}_j$$

其中 $y$ 是一个长度为 $n$ 的序列。

我们对后面的 $max$ 使用之前的式子：

调换求和顺序：

$min$ 是类似的。

证毕。

还有更强的：

$$\underset{i\in S}{\mathrm{kthmax}{x}_i}=\sum _{T\subseteq S}(-1{)}^{|T|-k}(\genfrac{}{}{0ex}{}{|T|-1}{k-1})\underset{j\in T}{min}{x}_j$$

$$\underset{i\in S}{\mathrm{kthmin}{x}_i}=\sum _{T\subseteq S}(-1{)}^{|T|-k}(\genfrac{}{}{0ex}{}{|T|-1}{k-1})\underset{j\in T}{max}{x}_j$$

$$E\left(\underset{i\in S}{\mathrm{kthmax}{x}_i}\right)=\sum _{T\subseteq S}(-1{)}^{|T|-k}(\genfrac{}{}{0ex}{}{|T|-1}{k-1})E\left(\underset{j\in T}{min}{x}_j\right)$$

$$E\left(\underset{i\in S}{\mathrm{kthmin}{x}_i}\right)=\sum _{T\subseteq S}(-1{)}^{|T|-k}(\genfrac{}{}{0ex}{}{|T|-1}{k-1})E\left(\underset{j\in T}{max}{x}_j\right)$$

规定若 ，则 ${\displaystyle (\genfrac{}{}{0ex}{}{n}{m})}=0$。

证明： 不妨设 。则有：

又因为有组合恒等式：${\displaystyle (\genfrac{}{}{0ex}{}{a}{b})}{\displaystyle (\genfrac{}{}{0ex}{}{b}{c})}={\displaystyle (\genfrac{}{}{0ex}{}{a}{c})}{\displaystyle (\genfrac{}{}{0ex}{}{a-c}{b-c})}$，所以有：

当 $i=n-k+1$ 时：

$$(\genfrac{}{}{0ex}{}{n-i}{k-1})\sum _{j=0}^{n-i-k+1}(\genfrac{}{}{0ex}{}{n-i-k+1}{j})(-1{)}^j=1$$

否则：

$$(\genfrac{}{}{0ex}{}{n-i}{k-1})\sum _{j=0}^{n-i-k+1}(\genfrac{}{}{0ex}{}{n-i-k+1}{j})(-1{)}^j=0$$

所以：

$$\sum _{i\in S}(\genfrac{}{}{0ex}{}{n-i}{k-1})x_i\sum _{j=0}^{n-i-k+1}(\genfrac{}{}{0ex}{}{n-i-k+1}{j})(-1{)}^j=\underset{i\in S}{\mathrm{kthmax}}{x}_i$$

剩下三个是类似的。

证毕。

根据 min-max 容斥，我们还可以得到下面的式子：

$$\underset{i\in S}{\mathrm{lcm}}{x}_i=\prod _{T\subseteq S}{\left(\underset{j\in T}{gcd}{x}_j\right)}^{(-1{)}^{|T|-1}}$$

因为 $\mathrm{lcm},gcd,a^1,a^{-1}$ 分别相当于 $max,min,+,-$，就是说相当于对于指数做了一个 min-max 容斥，自然就是对的了

PKUWC2018 随机游走

期望游走的步数也就是游走的时间。那么设随机变量 $x_i$ 表示第一次走到结点 $i$ 的时间。那么我们要求的就是

$$E\left(\underset{i\in S}{max}{x}_i\right)$$

使用 min-max 容斥可以得到

$$E\left(\underset{i\in S}{max}{x}_i\right)=E(\sum _{T\subseteq S}(-1{)}^{|T|-1}\underset{i\in T}{min}{x}_i)=\sum _{T\subseteq S}(-1{)}^{|T|-1}E\left(\underset{i\in T}{min}{x}_i\right)$$

对于一个集合 $T\in [n]$，考虑求出 $F(T)=E(\underset{i\in T}{min}{x}_i)$。

考虑 $E(\underset{i\in T}{min}{x}_i)$ 的含义，是第一次走到 $T$ 中某一个点的期望时间。不妨设 $f(i)$ 表示从结点 $i$ 出发，第一次走到 $T$ 中某个结点的期望时间。

• 对于 $i\in T$，有 $f(i)=0$。
• 对于 $i\notin T$，有 $f(i)=1+\frac{1}{\text{deg}(i)}\sum _{(i,j)\in E}f(j)$。

如果直接高斯消元，复杂度 $O(n^3)$。那么我们对每个 $T$ 都计算 $F(T)$ 的总复杂度就是 $O(2^n{n}^3)$，不能接受。我们使用树上消元的技巧。

不妨设根结点是 $1$，结点 $u$ 的父亲是 $p_u$。对于叶子结点 $i$，$f(i)$ 只会和 $i$ 的父亲有关（也可能 $f(i)=0$，那样更好）。因此我们可以把 $f(i)$ 表示成 $f(i)=A_i+B_{i}f(p_i)$ 的形式，其中 $A_i,B_i$ 可以快速计算。

对于非叶结点 $i$，考虑它的儿子序列 $j_1,\cdots ,j_k$。由于 $f(j_e)=A_{j_e}+B_{j_e}f(i)$。因此可以得到

$$f(i)=1+\frac{1}{\mathrm{deg}(i)}\sum _{e=1}^k(A_{j_e}+B_{j_e}f(i))+\frac{f(p_i)}{\mathrm{deg}(i)}$$

那么变换一下可以得到

$$f(i)=\frac{\mathrm{deg}(i)+\sum _{e=1}^k{A}_{j_e}}{\mathrm{deg}(i)-\sum _{e=1}^k{B}_{j_e}}+\frac{f(p_i)}{\mathrm{deg}(i)-\sum _{e=1}^k{B}_{j_e}}$$

于是我们把 $f(i)$ 也写成了 $A_i+B_{i}f(p_i)$ 的形式。这样可以一直倒推到根结点。而根结点没有父亲。也就是说

$$f(1)=\frac{\mathrm{deg}(1)+\sum _{e=1}^k{A}_{j_e}}{\mathrm{deg}(1)-\sum _{e=1}^k{B}_{j_e}}$$

解一下这个方程我们就得到了 $f(1)$，再从上往下推一次就得到了每个点的 $f(i)$。那么 $F(T)=f(x)$。时间复杂度 $O(n)$。

这样，我们可以对于每一个 $T$ 计算出 $F(T)$，时间复杂度 $O(2^{n}n)$。

回到容斥的部分，我们知道 $E(\underset{i\in S}{max}{x}_i)=\sum _{T\subseteq S}(-1{)}^{|T|-1}F(T)$。

不妨设 $F^{\prime }(T)=(-1{)}^{|T|-1}F(T)$，那么进一步得到 $E(\underset{i\in S}{max}{x}_i)=\sum _{T\subseteq S}{F}^{\prime }(T)$。因此可以使用 FMT（也叫子集前缀和，或者 FWT 或变换）在 $O(2^{n}n)$ 的时间内对每个 $S$ 计算出 $E(\underset{i\in S}{max}{x}_i)$，这样就可以 $O(1)$ 回答询问了。

习题

• ABC331- G - Collect Them All
• 洛谷 P4707 重返现世

参考文献

王迪《容斥原理》，2013 年信息学奥林匹克中国国家队候选队员论文集

Cyhlnj《有标号的 DAG 计数系列问题》

Wikipedia - 全序关系

本页面最近更新：2025/9/14 21:22:43，更新历史
发现错误？想一起完善？ 在 GitHub 上编辑此页！
本页面贡献者：Ir1d, sshwy, Enter-tainer, Tiphereth-A, Great-designer, MegaOwIer, Peanut-Tang, Xeonacid, CCXXXI, Chrogeek, ComeIntoCalm, HeRaNO, hsfzLZH1, iamtwz, Jerrycyx, Jiangkangping, kenlig, ksyx, Lumos-exe, lychees, megakite, ouuan, sbofgayschool, ShizuhaAki, StableAgOH, StudyingFather, tder6, untitledunrevised, UserUnauthorized, ZYStream
本页面的全部内容在 CC BY-SA 4.0 和 SATA 协议之条款下提供，附加条款亦可能应用