图的着色
点着色
(讨论的是无自环无向图)
对无向图顶点着色,且相邻顶点不能同色。若 G 是  - 可着色的,但不是
- 可着色的,但不是  - 可着色的,则称 k 是 G 的色数,记为
- 可着色的,则称 k 是 G 的色数,记为  。
。
对任意图 G,有  ,其中
,其中  为最大度。
为最大度。
Brooks 定理
设连通图不是完全图也不是奇圈,则  。
。
证明
证明
设  ,考虑数学归纳法。
,考虑数学归纳法。
首先, 时,命题显然成立。
时,命题显然成立。
接下来,假设对于  时的命题成立,下面我们要逐步强化命题。
时的命题成立,下面我们要逐步强化命题。
不妨只考虑  - 正则图,因为对于非正则图来说,可以看作在正则图里删去一些边构成的,而这一过程并不会影响结论。
- 正则图,因为对于非正则图来说,可以看作在正则图里删去一些边构成的,而这一过程并不会影响结论。
对于任意不是完全图也不是奇圈的正则图 G,任取其中一点 v,考虑子图  ,由归纳假设知
,由归纳假设知  ,接下来我们只需证明在 H 中插入 v 不会影响结论即可。
,接下来我们只需证明在 H 中插入 v 不会影响结论即可。
令  ,设 H 染的
,设 H 染的  种颜色分别为
种颜色分别为  ,v 的
,v 的  个邻接点为
个邻接点为  。不妨假设 v 的这些邻接点颜色两两不同,否则命题得证。
。不妨假设 v 的这些邻接点颜色两两不同,否则命题得证。
接下来我们设所有在 H 中染成  或
或  的点以及它们之间的所有边构成子图
的点以及它们之间的所有边构成子图  。不妨假设任意 2 个不同的点
。不妨假设任意 2 个不同的点  ,
, 一定在
一定在  的同一个连通分量中,否则若在两个连通分量中的话,可以交换其中一个连通分量所有点的颜色,从而
的同一个连通分量中,否则若在两个连通分量中的话,可以交换其中一个连通分量所有点的颜色,从而  ,
, 颜色相同。
颜色相同。
这里的交换颜色指的是若图中只有两种颜色 a,b,那么把图中原来染成颜色 a 的点全部染成颜色 b,把图中原来染成颜色 b 的点全部染成颜色 a。
我们设上述连通分量为  ,那么
,那么  一定只能是
一定只能是  到
到  的路。因为
的路。因为  在 H 中的度为
在 H 中的度为  ,所以
,所以  在 H 中的邻接点颜色一定两两不同,否则可以给
在 H 中的邻接点颜色一定两两不同,否则可以给  染别的颜色,从而和 v 的其他邻接点颜色重复,所以
染别的颜色,从而和 v 的其他邻接点颜色重复,所以  在
在  中邻接点数量为 1,
中邻接点数量为 1, 同理。然后我们在
同理。然后我们在  中取一条
中取一条  到
到  的路,令其为 P,若
的路,令其为 P,若  ,那么我们沿着 P 顺次给路上的点染色,设遇到的第一个度数大于 2 的点为 u,注意到 u 的邻接点最多只用了
,那么我们沿着 P 顺次给路上的点染色,设遇到的第一个度数大于 2 的点为 u,注意到 u 的邻接点最多只用了  种颜色,所以 u 可以重新染色,从而使
种颜色,所以 u 可以重新染色,从而使  ,
, 不连通。
不连通。
然后我们不难发现,对任意 3 个不同的点  ,
, ,
, ,
, 。
。
到这里我们对命题的强化工作就已经做完了。
接下来就很简单。首先,如果 v 的邻接点两两相邻,那么命题得证。不妨设  ,
, 不相邻,在
不相邻,在  中取
中取  的邻接点 w,交换
的邻接点 w,交换  中的颜色。得到的新图中,
中的颜色。得到的新图中, ,矛盾。
,矛盾。
至此命题证明完毕。
Welsh–Powell 算法
Welsh–Powell 算法是一种在 不限制最大着色数 时寻找着色方案的贪心算法。
对于无自环无向图 G,设  满足。
满足。

按 Welsh–Powell 算法着色后的颜色数至多为  , 该算法的时间复杂度为
, 该算法的时间复杂度为  。
。
过程
- 将当前未着色的点按度数降序排列。
- 将第一个点染成一个未被使用的颜色。
- 顺次遍历接下来的点,若当前点和所有与第一个点颜色 相同 的点 不相邻,则将该点染成与第一个点相同的颜色。
- 若仍有未着色的点,则回到步骤 1, 否则结束。
示例如下:
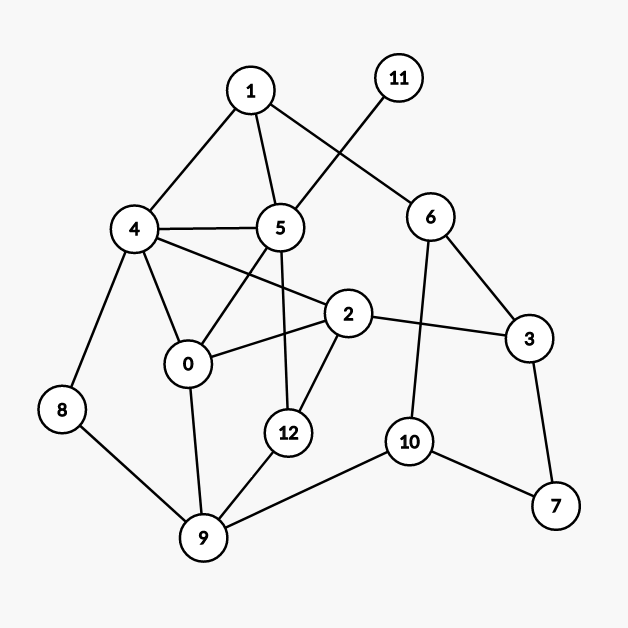
(由 Graph Editor 生成)
我们先对点按度数降序排序,得:
| 次序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|
| 点的编号 | 4 | 5 | 0 | 2 | 9 | 1 | 3 | 6 | 10 | 12 | 7 | 8 | 11 |
| 度数 | 5 | 5 | 4 | 4 | 4 | 3 | 3 | 3 | 3 | 3 | 2 | 2 | 1 |
 | 1 | 2 | 3 | 4 | 5 | 4 | 4 | 4 | 4 | 4 | 3 | 3 | 2 |
所以 Welsh–Powell 算法着色后的颜色数最多为 5。
另外因为该图有子图  , 所以色数一定大于等于 3。
, 所以色数一定大于等于 3。
第一次染色:
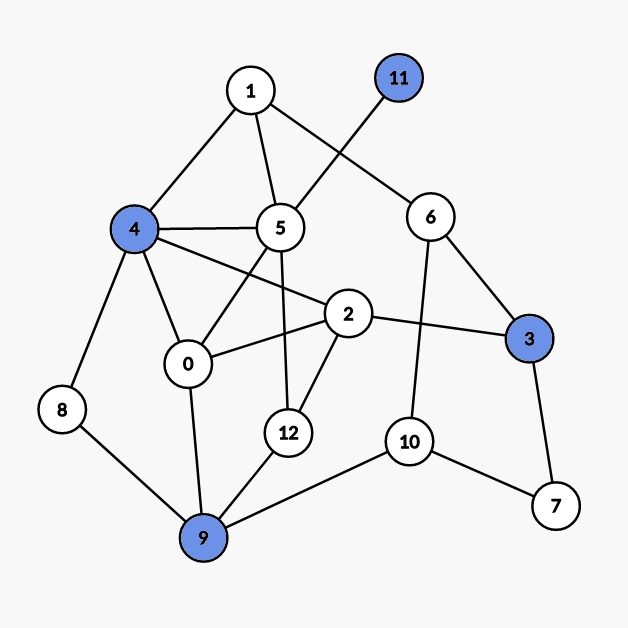
染 4 9 3 11 号点。 - 第二次染色:
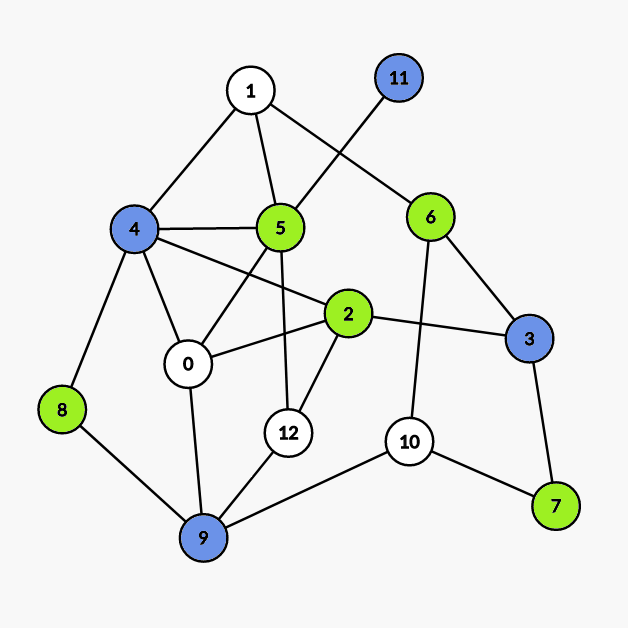
染 5 2 6 7 8 号点。 - 第三次染色:
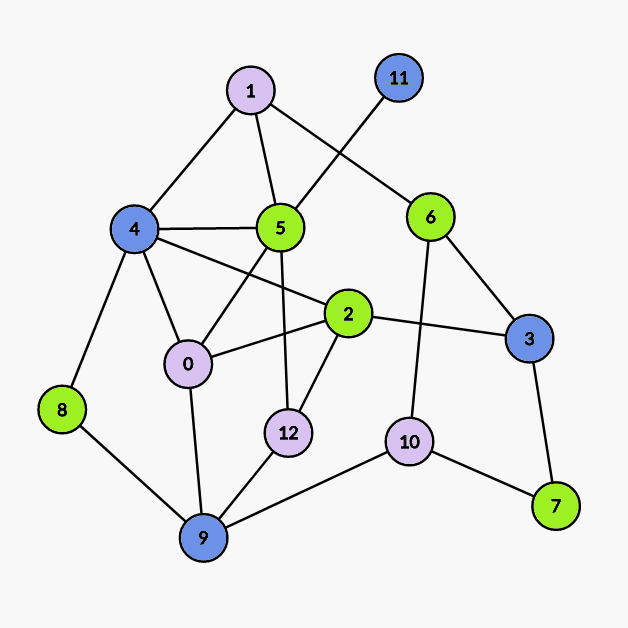
染 0 1 10 12 号点。
证明
证明
对于无自环无向图 G,设  满足
满足

令  , 我们取
, 我们取  中的子集
中的子集  , 其中的元素满足
, 其中的元素满足
 , 其中
, 其中 
若

则  当且仅当
当且仅当

 与
与  均不相邻
均不相邻
显然若将  中的点染成第 i 种颜色,则该染色方案即为 Welsh–Powell 算法给出的方案,显然有
中的点染成第 i 种颜色,则该染色方案即为 Welsh–Powell 算法给出的方案,显然有
我们只需要证明:

其中

上式左边的不等号显然成立,我们考虑右边。
首先我们不难得出:
若  ,则 v 与
,则 v 与  中分别至少有一个点相邻,从而有
中分别至少有一个点相邻,从而有 
进而

另一方面,基于序列  的构造方法,我们不难发现
的构造方法,我们不难发现

两式结合即得证。
边着色
对无向图的边着色,要求相邻的边涂不同种颜色。若 G 是 k- 边可着色的,但不是  - 边可着色的,则称 k 是 G 的边色数,记为
- 边可着色的,则称 k 是 G 的边色数,记为  。
。
Vizing 定理
设 G 是简单图,则 
若 G 是二部图,则 
当  为奇数(
为奇数( )时,
)时, ; 当
; 当  为偶数时,
为偶数时,
二分图 Vizing 定理的构造性证明
证明
按照顺序在二分图中加边。
我们在尝试加入边  的时候,我们尝试寻找对于
的时候,我们尝试寻找对于  和
和  的编号最小的尚未被使用过的颜色,假设分别为
的编号最小的尚未被使用过的颜色,假设分别为  和
和  。
。
如果  此时我们可以直接将这条边的颜色设置为
此时我们可以直接将这条边的颜色设置为  。
。
否则假设  , 我们可以尝试将节点
, 我们可以尝试将节点  连出去的颜色为
连出去的颜色为  的边的颜色修改为
的边的颜色修改为  。
。
修改的过程可以被近似的看成是一条从  出发,依次经过颜色为
出发,依次经过颜色为  的边的有限唯一增广路。
的边的有限唯一增广路。
因为增广路有限所以我们可以将增广路上所有的边反色,即原来颜色为  的修改为
的修改为  ,原来颜色为
,原来颜色为  的修改为
的修改为  。
。
根据二分图的性质,节点  不可能为增广路节点,否则与最小未使用颜色为
不可能为增广路节点,否则与最小未使用颜色为  矛盾。
矛盾。
所以我们可以在增广之后直接将连接  和
和  的边的颜色设为
的边的颜色设为  。
。
总构造时间复杂度为  。
。
示例代码 UVa10615 Rooks
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123 | #include <iostream>
constexpr int MAXN = 100;
int t;
int n;
char a[MAXN + 10][MAXN + 10];
int c[MAXN + 10][MAXN + 10];
int ans;
namespace graph {
struct Vertex {
int head;
int deg;
int vis[MAXN + 10];
} vertex[2 * MAXN + 10], e;
struct Edge {
int head;
int next;
int col;
} edge[2 * MAXN * MAXN + 10];
int ecnt;
void init() {
for (int i = 0; i < MAXN + 10; i++) std::fill(c[i], c[i] + MAXN + 10, 0);
for (int i = 1; i <= 2 * MAXN; i++) vertex[i] = e;
for (int i = 0; i <= 2 * MAXN * MAXN; i++) edge[i].col = 0;
ecnt = 1;
ans = 0;
return;
}
void addEdge(int tail, int head) {
ecnt++;
edge[ecnt].head = head;
edge[ecnt].next = vertex[tail].head;
vertex[tail].head = ecnt;
vertex[tail].deg++;
return;
}
int get(int u) {
for (int i = 1; i <= n; i++)
if (!vertex[u].vis[i]) return i;
exit(1);
}
void DFS(int u, int ori, int upd) {
if (vertex[u].vis[ori] == 0) {
vertex[u].vis[upd] = 0;
return;
}
int e = vertex[u].vis[ori];
int v = edge[e].head;
DFS(v, upd, ori);
edge[e].col = upd;
edge[e ^ 1].col = upd;
vertex[u].vis[upd] = e;
vertex[v].vis[upd] = e ^ 1;
return;
}
void AddEdge(int u, int v) {
addEdge(u, v);
addEdge(v, u);
return;
}
void solve() {
for (int u = 1; u <= n; u++) {
for (int e = vertex[u].head; e; e = edge[e].next) {
int v = edge[e].head;
if (edge[e].col) continue;
int lu = get(u);
int lv = get(v);
if (lu < lv) DFS(v, lu, lv);
if (lu > lv) DFS(u, lv, lu);
int l = std::min(lu, lv);
vertex[u].vis[l] = e;
vertex[v].vis[l] = e ^ 1;
edge[e].col = l;
edge[e ^ 1].col = l;
}
}
}
void generate() {
for (int u = 1; u <= n; u++) {
for (int e = vertex[u].head; e; e = edge[e].next) {
int v = edge[e].head;
c[u][v - n] = edge[e].col;
}
}
return;
}
} // namespace graph
void mian() {
graph::init();
std::cin >> n;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) std::cin >> a[i][j];
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (a[i][j] == '*') graph::AddEdge(i, j + n);
for (int i = 1; i <= n * 2; i++) ans = std::max(ans, graph::vertex[i].deg);
graph::solve();
graph::generate();
std::cout << ans << '\n';
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) std::cout << c[i][j] << ' ';
std::cout << '\n';
}
return;
}
int main() {
std::cin >> t;
while (t--) mian();
return 0;
}
|
一道很不简单的例题 uoj 444 二分图
本题为笔者于 2018 年命制的集训队第一轮作业题。
首先我们可以发现答案下界为度数不为 k 倍数的点的个数。
下界的构造方法是对二分图进行拆点。
若  , 我们将其拆为
, 我们将其拆为  个度数为 k 的节点和一个度数为
个度数为 k 的节点和一个度数为  的节点。
的节点。
若  , 我们将其拆为
, 我们将其拆为  个度数为 k 的节点。
个度数为 k 的节点。
拆出来的点在原图中的意义相同,也就是说,在满足度数限制的情况下,一条边端点可以连接任意一个拆出来的点。
根据 Vizing 定理,我们显然可以构造出该图的一种 k 染色方案。
删边部分由于和 Vizing 定理关系不大这里不再展开。
有兴趣的读者可以自行阅读笔者当时写的题解。
色多项式
 表示 G 的不同 k 着色方式的总数。
表示 G 的不同 k 着色方式的总数。


在无向无环图 G 中,
 ,则
,则 
 ,则
,则 
定理:设  是 G 的点割集,且
是 G 的点割集,且 ![G[V_1]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7) 是 G 的
是 G 的  阶完全子图,
阶完全子图, 有
有  个连通分支,则:
个连通分支,则:
![P(G,k)=\frac{\Pi_{i=1}^{p}{(P(H_i, k))}}{P(G[V_1], k)^{p-1}}](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
其中 ![H_i=G[V_1 \cup V(G_i)]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
参考资料
- Graph coloring - Wikipedia
- Welsh, D. J. A.; Powell, M. B. (1967), "An upper bound for the chromatic number of a graph and its application to timetabling problems", The Computer Journal, 10 (1): 85–86
本页面最近更新:2024/3/27 06:46:12,更新历史
发现错误?想一起完善? 在 GitHub 上编辑此页!
本页面贡献者:Chrogeek, CoderOJ, Enter-tainer, iamtwz, ImpleLee, Ir1d, lyccrius, ouuan, Tiphereth-A, zhouyuyang2002
本页面的全部内容在 CC BY-SA 4.0 和 SATA 协议之条款下提供,附加条款亦可能应用



